はじめに
こんにちは、お疲れ様です。
最近暑くて、食欲がない今日この頃です。夏バテに気をつけていきましょう。
本日は、円柱でも作ろうかなと思っています。明らかに量が多くなりそうなので、前半後半に分ける前提で作業をしようかと思っています。よろしくお願いいたします。
簡単に、円柱って側面と二つの底面で構成されているので、前半を側面パート後半を底面パートにしていこうかと思っています。
/src
└ /object
└ cylinder.rsクラス図
円柱(Cylinder)を下記のイメージで作っていこうと思います。交差判定を今まで通りintersectに詰め込むと大変なことになりそうなので、分けて実装しようかと思います。また、交差点における法線の算出も割と複雑になりそうなので、今回は分けることにします。normal_atに関しては、Shapeの方で定義しておいてもいい気がします。

Cylinderの実装
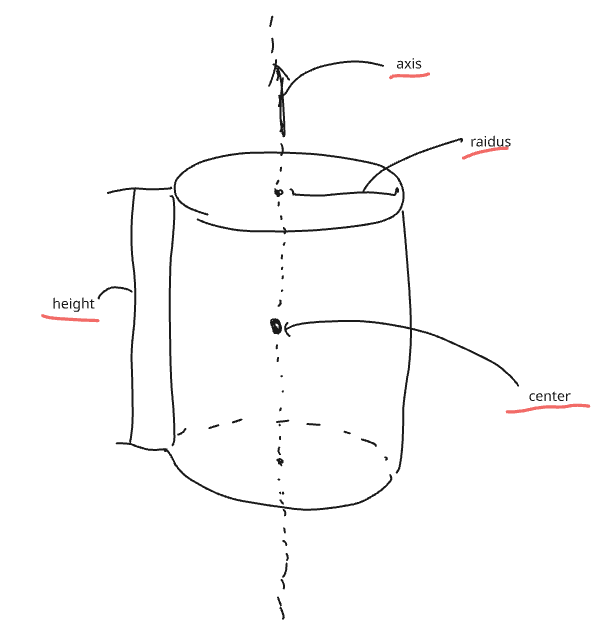
何はともあれ、初めにデータ構造を定義しないと始まらないので定義していきます。絵心ないのは許して欲しいですが、円柱を描写する時に必要なデータ構造はおそらく、半径、高さ、円柱の中心、円柱の軸の4つかなと思います。
上記をもとに、データ構造を定義すると下記のような感じになるかと思います。
pub struct Cylinder {
pub center: Point3, // 円柱の軸の中央に位置する点
pub axis: Vector3,
pub radius: f64,
pub height: f64,
}
impl Cylinder {
pub fn new(center: Point3, axis: Vector3, radius: f64, height: f64) -> Self {
let normalized_axis = axis.unit();
Self {
center,
axis: normalized_axis,
radius,
height,
}
}
fn intersect_side(&self, ray: &Ray, t_min: f64, t_max: f64) -> Option<f64> {
//TODO
}
fn intersect_caps(&self, ray: &Ray, t_min: f64, t_max: f64) -> Option<f64> {
//TODO
}
fn nomal_at(&self, point: &Point3) -> Vector3 {
//TODO
}
}円柱の側面の交差判定
円柱の側面の条件は、下記2つを満たせば良いのかと思います。
・1: 軸からの距離が半径r上にある。
・2: 円柱の高さに収まっている。
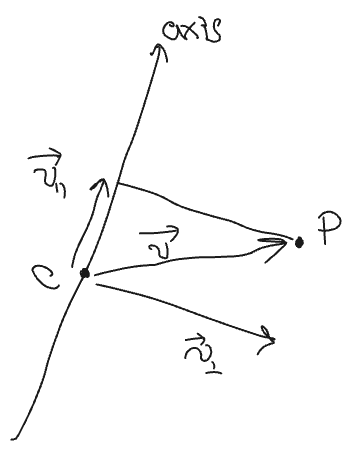
1について、\( \vec{v_{\perp}} \)の長さが、半径rであることの確認。
2について、\( \vec{v_{||}} \)がCを中心に高さheight以内に収まっていることの確認。
上記を達成すれば、うまく描写されるはずです。
1: 軸からの距離が半径r上にある。
\( \vec{axis}\)が単位ベクトルとし、\( \vec{v_{||}} = (\vec{v}, \vec{axis}) * \vec{axis} \)で算出できるので、\( \vec{v_{\perp}} = \vec{v} – \vec{v_{||}} = \vec{v} – (\vec{v}, \vec{axis}) * \vec{axis} \)で計算できます。
これをもとに、\( vec{v} = \vec{R(t)} – \vec{C} \)と半径がrであることを用いて下記のtの方程式をとければ良い良いのかと思います。
(\(R(t) = \vec{O} + t * \vec{D}\), Oは光線ベクトルの始点、Dは光線の方向ベクトル)
$$
d(t)^2 = || (\vec{R(t)} – \vec{C}) – (\vec{R(t)} – \vec{C}, \vec{axis}) * \vec{axis} ||^2 = r^2
$$
こちらを頑張って展開していきます。\(R(t) = \vec{O} + t * \vec{D} \)を実際に代入して、\( \vec{CO} = \vec{O} – \vec{C} \)としつつ計算進めると下記になります。
$$
r^2 = || \vec{CO_{\perp}} – t * \vec{D_{\perp}}||^2 \\\ = || \vec{CO_{\perp}}||^2 + 2t(\vec{CO_{\perp}},\vec{D_{\perp}}) + t^2 ||\vec{D_{\perp}} ||^2
$$
tの2次元の方程式に落とし込めたので、判別式\(\Delta\)を用いて解の有無で交差判定をしていきます。
$$
\Delta = (2 (\vec{CO_{\perp}},\vec{D_{\perp}})) ^2 – 4 ||\vec{D_{\perp}} ||^2 (|| \vec{CO_{\perp}}||^2 – r^2)
$$
補足
$$
\vec{CO_{\perp}} = \vec{CO} – (\vec{CO}, \vec{axis}) \vec{axis}
$$
$$
\vec{D_{\perp}} = \vec{D} – (\vec{D}, \vec{axis}) \vec{axis}
$$
2: 円柱の高さに収まっている。
上記を読み進めることができたのであれば、ここの判定は容易です。
上記にある\( \vec{v_{||}} = (\vec{v}, \vec{axis}) * \vec{axis} \)をベースに考えればすぐです。
\(p\)をヒットしたとし\( \vec{v} = \vec{p} – \vec{c} \)とすると、\( \vec{cp_{||}} = (\vec{cp}, \vec{axis}) * \vec{axis} \)となります。
\(\vec{cp}\)の\(\vec{axis}\)への射影であるので、この値が、\( height/2\)以下であることを確認すればOKです。
実装するぞー
上記をもとに実装を進めます。
fn intersect_side(&self, ray: &Ray, t_min: f64, t_max: f64) -> Option<f64> {
let co = ray.get_origin() - self.center;
let dir_dot_axis = ray.get_direction().dot(&self.axis);
let co_dot_axis = co.dot(&self.axis);
let dir_perp = ray.get_direction() - dir_dot_axis * self.axis;
let co_perp = co - co_dot_axis * self.axis;
let a = dir_perp.length_squared();
// aが0だとそもそも2次方程式の会の公式の分母が0になるので計算できない。
if a < f64::EPSILON {
return None;
}
let b = 2.0 * co_perp.dot(&dir_perp);
let c = co_perp.length_squared() - self.radius * self.radius;
let d = b * b - 4.0 * a * c;
// 判別式dが0未満の場合、解なし=交差点が存在しない
if d < 0.0 {
return None;
}
let sqrt_d = d.sqrt();
let mut t1 = (- b - sqrt_d) / (2.0 * a);
let mut t2 = (- b + sqrt_d) / (2.0 * a);
//tの範囲のチェック
if t1 > t_max || t2 < t_min {
return None;
}
if t1 < t_min {
t1 = t_min;
}
if t2 > t_max {
t2 = t_max;
}
// 円柱の高さ以内に収まっているか?
let check_height = |t: f64| -> bool {
let hit_point = ray.at(t);
let hit_height = (hit_point - self.center).dot(&self.axis);
hit_height.abs() <= self.height / 2.0
};
if check_height(t1) {
Some(t1)
} else if check_height(t2) {
Some(t2)
} else {
None
}
}法線ベクトルの算出
こちらもあまり、難しくはないです。交差した点をPとして\(\vec{CP_{\perp}}\)を求めることができればOKです。つまり、下記で求めればおおけーです。これに加えて高さに気をつければ良いでしょう。
$$
\vec{PC_{\perp}} = \vec{PC} – (\vec{PC}, \vec{axis}) \vec{axis}
$$
fn normal_at(&self, point: &Point3) -> Vector3 {
// 側面の法線求める
let pc = *point - self.center;
let axis_projection = pc.dot(&self.axis);
let axis_component = axis_projection * self.axis;
// 今回は底面の交差判定をしていないが、底面にある時はここに入る。
if (axis_projection.abs() - self.height / 2.0).abs() < 1e-8 {
if axis_projection > 0.0 {
return self.axis;
} else {
return -self.axis;
}
}
let normal = pc - axis_component;
normal.unit()
}Shapeのintersectを実装する
このまま動作確認と行きたいですが、下記を追加しないと怒られます(泣)。
impl Shape for Cylinder {
fn intersect(&self, ray: &Ray, t_min: f64, t_max: f64) -> Option<Intersection> {
let side_intersection = self.intersect_side(ray, t_min, t_max);
let t = match(side_intersection) {
(Some(t_side)) => t_side,
(None) => return None,
};
if t < t_min || t > t_max {
return None;
}
let hit_point = ray.at(t);
let normal = self.normal_at(&hit_point);
let mut intersection = Intersection {
t,
point: hit_point,
normal,
front_face: false,
};
intersection.set_face_normal(ray, normal);
Some(intersection)
}
}動作確認
動作確認用に下記を用意しました。足りない、パッケージは、追加してください。
動作確認用main.rs
pub fn main() -> Result<(), Box<dyn Error>> {
let width = 256;
let height = 256;
let film = Film::new(width, height);
let pos = Point3::new(0.0, 0.5, 3.0);
let look_at = Point3::new(0.0, 0.5, -1.0);
let up = Vector3::new(0.0, 1.0, 0.0);
let fov = 90.0_f64.to_radians();
let mut cam = Camera::new(pos, look_at, up, fov, film);
let mut scene = Scene::new();
scene.add(Box::new(Cylinder::new(
Point3::new(1.5, 1.0, -1.0),
Vector3::new(0.0, 0.25, -1.0),
1.0,
2.0,
)));
scene.add(Box::new(Cylinder::new(
Point3::new(-1.5, 1.0, -1.0),
Vector3::new(0.0, 1.0, 0.0),
1.0,
2.0,
)));
for y in 0..height {
for x in 0..width {
let u = x as f64 / (width - 1) as f64;
let v = y as f64 / (height - 1) as f64;
let ray = cam.generate_ray(u, v);
let mut color = Color3::zero();
if let Some((_, intersection)) = scene.intersect(&ray, f64::EPSILON, f64::INFINITY) {
let normal = intersection.normal;
color = Rgb::new(
0.5 * (normal.get_x() + 1.0),
0.5 * (normal.get_y() + 1.0),
0.5 * (normal.get_z() + 1.0),
);
} else {
let unit_direction = ray.get_direction().unit();
let t = 0.5 * (unit_direction.get_y() + 1.0);
let white = Rgb::new(1.0, 1.0, 1.0);
let blue = Rgb::new(0.5, 0.7, 1.0);
color = white*(1.0 - t) + blue*t;
}
cam.record_pixel(x, y, color);
}
}
let ppm_output = PpmOutput;
ppm_output.save(cam.get_film(), "build/cylinder_test.ppm").unwrap();
Ok(())
}上記を実行して、下記が出力されればOKです。
今回は、底面を実装していないので、空洞であることの確認と、側面からの確認ですね!
お疲れ様でした。

さいごに
お疲れ様でした。次は、底面でも追加しようかと思います。
よろしくお願いいたします。

