[Rust] レイトレーシング – 2

はじめに

お疲れ様です。
先日、と言っても一週間前ですが、下記でTuple3を作りました。今日は、Vector3のクラスを作っていきたいと思います。数学苦手だぁって人はオェーってなるかもしれないですが、詳細なことは省くので許して欲しいです。

前回のやつはこちらです。こだわりがなければ、実装をまとめてしまってもいいかもしれないです。

ひとまず、必要なベクトルの計算

ベクトルに関する計算であったら便利だなぁと言ったものをまとめます。

• ベクトルの大きさ
• 単位ベクトル
• 内積
• 外積

まず、ベクトルってなんだっけって人もいると思います。ひとまず、下の矢印をイメージすれば良いと思います。下記を見つつ、補足していきます。
ベクトルの大きさは矢印の長さです。
また、単位ベクトルは長さが　1　のベクトルの呼称です。
（単位ベクトルは、大きさはいらんけど方向は知りたいなぁってときに割と役に立つので重宝します。）

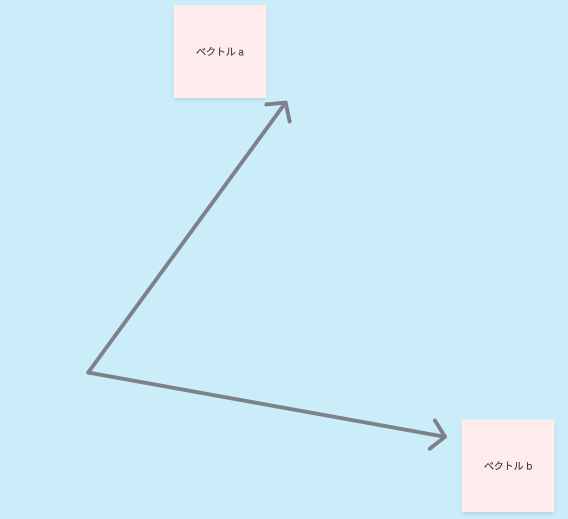
次に、内積と外積ですね。これらは、イメージがつきづらいかもしれないです。
下の図を見ながらイメージを固めていきたいと思います。
まず、内積についてです。こちらのイメージは、ベクトルaとベクトルbがどれだけ仲良しかを調べるための値です。大きければ仲良して、マイナスだと喧嘩しているような感じです。

次に外積ですが、２つのベクトルに垂直なベクトルのことをいいます。一つに定まらないと思うかもしれないですが、右ねじの向きのベクトルです。例えば、ベクトルbを基準に考えたとするとディスプレイから読者方向のベクトルとなります。

Vector3を実装する

次に, 今日は下記の部分を作っていきます。

my_rendere
└ src
  ┝ util
  │ ┝ vector.rs (new)
  │ ┝ color.rs (new 次節)
  │ ┝ tuple3.rs
  │ └ vector
  │ │└ vector.rs (new)
  │ └ color
  │    ┝ color.rs (new　次節)
  │    └ rgb_color.rs (new 次節)
　┝ main.rs
  └ util.rs

// src/util/vector.rs
pub mod vector3;

vector.rsの方は下記で作っていきます。前節の計算以外にもいくつか追加実装します。

use crate::util::tuple3::Tuple3;

pub type Vector3 = Tuple3; // +, -, *, /は共通なのでベースをこれにします。

impl Vector3 {
    // xの要素を取得
    pub fn get_x(&self) -> f64 {
        self.e[0]
    }
    // yの要素を取得
    pub fn get_y(&self) -> f64 {
       self.e[1]
    }
    // zの要素を取得
    pub fn get_z(&self) -> f64 {
       self.e[2]
    }
    // 内積計算
    pub fn dot(&self, other: &Vector3) -> f64 {
        self.e[0]* other.e[0] + self.e[1] * other.e[1] + self.e[2] * other.e[2]
    }
    // 長さの2乗
    pub fn length_squared(&self) -> f64 {
        self.dot(self)
    }
    // ベクトルの長さ
    pub fn length(&self) -> f64 {
        self.length_squared().sqrt()
    }
    // 単位ベクトル
    pub fn unit(&self) -> Vector3 {
        let norm = self.length();
        if norm > f64::EPSILON {
            *self / norm
        } else {
            *self
        }
    }
    // 外積
    pub fn cross(&self, other: &Vector3) -> Vector3{
        Vector3::new (
            self.e[1] * other.e[2] - self.e[2] * other.e[1],
            self.e[2] * other.e[0] - self.e[0] * other.e[2],
            self.e[0] * other.e[1] - self.e[1] * other.e[0],
        )
    } 
}

pub type Point3 = Vector3; // 型で点なのかベクトル目的なのか分かりやすくしたいだけです。

お疲れ様です。内積や外積の計算間違えると将来苦労します。内積でミスっていると表面なのか裏側なのかの判定がバグります。外積の計算を間違えると表示の際に反転してしまったりして大変です。恥ずかしながら実体験ですが、、、

Vector3の確認しましょう！

fn main() {
    let a = Vector3::new(1.0, 2.0, 3.0);
    let b = Vector3::new(-1.0, 1.0, 2.0);

    println!("length: {}", a.length());
    println!("unit  : {:?}", a.unit());
    println!("dot   : {}", a.dot(&b));
    
    let c = a.cross(&b);
    println!("cross : {:?}", c);
    println!("a·c   : {:?}", a.dot(&c)); // cがaとbに対して垂直なので0.0になるはず！
    println!("b·c   : {:?}", b.dot(&c));
}

下記で出力されたら、OKです。

Colorを実装する

色の設定を簡単にします。

// color.rs
use crate::util::tuple3::Tuple3;

#[derive(Debug)]
pub enum ColorSystem {
    RGB,
    None,
}

pub trait ColorSpace {
    fn get_color_space() -> ColorSystem;
}

pub type Color3 = Tuple3;

正直必要になるかわからないですが、念の為作ろうかと思っています。将来的にRGBだけではなく、XYZやLabなども実装できたらいいなと思っているので、作っています。

当分はRgbしか考慮しないと思うので、ひとまずこんな感じで作ろうと思います。将来的に増えた時にまた改めて考えます。

// rgb_color
use super::color::{Color3, ColorSystem, ColorSpace};

pub type Rgb = Color3;

impl Rgb {
    pub fn get_r(&self) -> f64 {
        self.e[0]
    }
    pub fn get_g(&self) -> f64 {
        self.e[1]
    }
    pub fn get_b(&self) -> f64 {
        self.e[2]
    }
}

impl ColorSpace for Rgb {
    fn get_color_space() -> ColorSystem {
        ColorSystem::RGB
    }
}

おわりに

お疲れ様です。今日は、ベクトルの計算を中心に扱いました。次は、Rayの定義だったり、CameraModelの定義をしていけたらと思います。
来週も仕事頑張るぞー。