はじめに
お疲れ様です。本日は、三角形を表示できるようにしていこうかと思っています。よろしくお願いいたします。先週投稿するつもりでしたが、思ったより長くなって、途中で挫折しました。情けない限りです、、、
今日の追加予定は、下記です。
/src
└ /object
└ triangle.rsクラス図
今回は、クラス間の関係性を明記する必要はないかもしれないですがなんとなく追加しておきます。
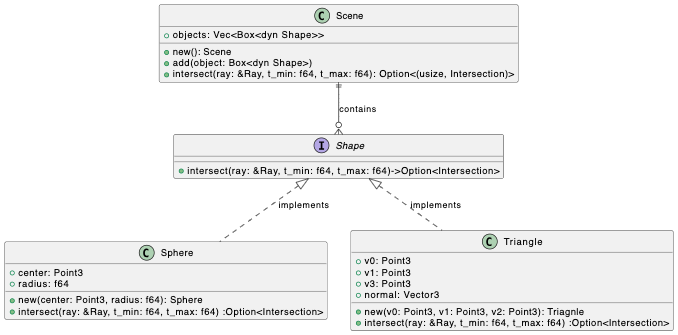
Triangleの実装
恒例になりつつありますが、何があれば、三角形として表現する上で十分か考えていきます。
パッと思いつくのは、頂点の座標が確定すれば、表現できると思います。
ついでに、光の3点から法線を事前に持っておけば計算量を抑えられるかもしれないので、法線も保持しておきます。前回の球は、交差点から都度求める必要がありますが、三角形や平面は、交差点の位置によらず一定なので、事前に求めておいても良いかと思った次第です。
ひとまず、データ構造の定義と初期化部分を作っていきます。
pub struct Triangle {
pub v0: Point3, // 頂点0
pub v1: Point3, // 頂点1
pub v2: Point3, // 頂点2
pub normal: Vector3, // 三角形の法線
}
impl Triangle {
pub fn new(v0:Point3, v1:Point3, v2:Point3) -> Self {
//辺ベクトル
let edge1 = v1 - v0;
let edge2 = v2 - v0;
//2辺のベクトルの外積計算で法線が計算できるって寸法よ!
let normal = edge1.cross(&edge2).unit();
Triangle {v0, v1, v2, normal}
}
}次に交差判定部分を作っていきます。方針としては、三角形上に\(Ray(t)=\vec{origin} + t * \vec{dir} \)で表現できる\( t \)が存在することを計算で求めていきます。
まず、三角形上の点はどう表現するか?から始めていきます。三角形上の点\( P \)は、下記で表現できます。証明は、、、今回省きます。「三角形、重心座標」とかで調べたら出てくるとは思います。
$$P = (1 – u – v) * \vec{v_0} + u * \vec{v_1} + v * \vec{v_2}$$$$P = \vec{v_0} + u * (\vec{v_1} – \vec{v_0}) + v * (\vec{v_2} – \vec{v_0})$$$$ (u >= 0, v >= 0, u+v<=1)$$
\( Ray(t)=\vec{origin} + t * \vec{dir} \)と合わせて考えると下記となる。(\( \vec{edge_1} = \vec{v_1} – \vec{v_0}\), \( \vec{edge_2} = \vec{v_2} – \vec{v_0}\)とする。)
$$Ray(t)=\vec{origin} + t * \vec{dir} = \vec{v_0} + u * \vec{edge_1} + v * \vec{edge_2}$$$$\vec{origin} – \vec{v_0} = – t * \vec{dir} + u * \vec{edge_1} + v * \vec{edge_2}$$
さらに、まとめていく。(\( \vec{s} = \vec{origin} – \vec{v_0}\)とする)
$$\vec{s} = (-\vec{dir},\vec{edge_1},\vec{edge_2})(t,u,v)^\top$$
↑縦ベクトルがうまくできなかったので、転置表現で逃げた、、、申し訳ないです。
連立方程式を解けば、\(t, u, v\)を求めることができますが、面倒なので、クラメルの公式を使っていきます。クラメルの公式自体は、行列なので、大学の線形代数履修したことがある方は、馴染み深いかもしれないです。
\((t,u,v)^\top \\= \frac{1}{|-\vec{dir},\vec{edge_1},\vec{edge_2}|}(|\vec{s},\vec{edge_1},\vec{edge_2}|,|-\vec{dir},\vec{s},\vec{edge_2}|,|-\vec{dir},\vec{edge_1},\vec{s}|)^\top\)
これを下記の補足を使って、頑張って整理すると最終的には、次で\(t, u, v\)を計算できます。
補足
\( |\vec{A}, \vec{B}, \vec{C}| \\= ((\vec{A} \times \vec{B}), \vec{C}) = -((\vec{B} \times \vec{A}), \vec{C}) \\= ((\vec{B} \times \vec{C}), \vec{A}) = -((\vec{C} \times \vec{B}), \vec{A}) \\= ((\vec{C} \times \vec{A}), \vec{B}) = -((\vec{A} \times \vec{C}), \vec{B})\)
\((t,u,v)^\top \\= \frac{1}{((\vec{dir} \times \vec{edge_2}),\vec{edge_1})}(((\vec{s} \times \vec{edge_1}),\vec{edge_2}),((\vec{dir} \times \vec{edge_2}),\vec{s}), ((\vec{s}\times \vec{edge_1}),\vec{dir}))^\top\)
\(
t = \frac{((\vec{s} \times \vec{edge_1}),\vec{edge_2})}{((\vec{dir} \times \vec{edge_2}),\vec{edge_1})},
u = \frac{((\vec{dir} \times \vec{edge_2}),\vec{s})}{((\vec{dir} \times \vec{edge_2}),\vec{edge_1})},
v = \frac{((\vec{s}\times \vec{edge_1}),\vec{dir})}{((\vec{dir} \times \vec{edge_2}),\vec{edge_1})}
\)
長くなりましたが、この結果をもとに実装をしていきます。
impl Shape for Triangle {
fn intersect(&self, ray: &Ray, t_min: f64, t_max: f64) -> Option<Intersection> {
let edge1 = self.v1 - self.v0;
let edge2 = self.v2 - self.v0;
let h = ray.get_direction().cross(&edge2);
let a = edge1.dot(&h);
// 分母が0の時は、計算できないのでチェックする
if a.abs() < f64::EPSILON {
return None;
}
let f = 1.0 / a;
let s = ray.get_origin() - self.v0;
let u = f * s.dot(&h);
// uの条件は、0.0 <= u <= 1.0
if u < 0.0 || u > 1.0 {
return None;
}
let q = s.cross(&edge1);
let v = f * ray.get_direction().dot(&q);
// 次の条件を満たす必要がある。0.0 <= v <= 1.0, u + v <= 1.0
// ここの時点で0.0 <= u <= 1.0であることを保証されている。
if v < 0.0 || u + v > 1.0 {
return None;
}
let t = f * edge2.dot(&q);
// tの範囲に収まっているか?
if t < t_min || t > t_max {
return None;
}
// ここまで処理されていれば、交差点を持っている。
// 交差点とその時の法線を求める。
let point = ray.at(t);
let mut intersection = Intersection {
t,
point,
normal: self.normal,
front_face: false,
};
intersection.set_face_normal(ray, self.normal);
Some(intersection)
}
}動作の確認
ここまで、来れた方はおそらく猛者ですね、、自分で書いていてなんですが、やばそうだなと思っていました。次で実行確認できたら終了です。
pub fn main() -> Result<(), Box<dyn Error>> {
let width = 256;
let height = 256;
let film = Film::new(width, height);
let pos = Point3::new(0.0, 0.5, 1.0);
let look_at = Point3::new(0.0, 0.5, -1.0);
let up = Vector3::new(0.0, 1.0, 0.0);
let fov = 90.0_f64.to_radians();
let mut cam = Camera::new(pos, look_at, up, fov, film);
let mut scene = Scene::new();
scene.add(Box::new(Plane::new(
Point3::new(0.0, 0.0, 0.0),
Vector3::new(0.0, 1.0, 0.0),
)));
scene.add(Box::new(Triangle::new(
Point3::new(0.0, 1.0, -1.0),
Point3::new(1.0, 0.0, -1.0),
Point3::new(-1.0, 0.0, -1.0),
)));
for y in 0..height {
for x in 0..width {
let u = x as f64 / (width - 1) as f64;
let v = y as f64 / (height - 1) as f64;
let ray = cam.generate_ray(u, v);
let mut color = Color3::zero();
if let Some((_, intersection)) = scene.intersect(&ray, f64::EPSILON, f64::INFINITY) {
let normal = intersection.normal;
color = Rgb::new(
0.5 * (normal.get_x() + 1.0),
0.5 * (normal.get_y() + 1.0),
0.5 * (normal.get_z() + 1.0),
);
} else {
let unit_direction = ray.get_direction().unit();
let t = 0.5 * (unit_direction.get_y() + 1.0);
let white = Rgb::new(1.0, 1.0, 1.0);
let blue = Rgb::new(0.5, 0.7, 1.0);
color = white*(1.0 - t) + blue*t;
}
cam.record_pixel(x, y, color);
}
}
let ppm_output = PpmOutput;
ppm_output.save(cam.get_film(), "build/triangle_test.ppm").unwrap();
Ok(())
}上記の期待値は、次の画像が出力されていれば問題なさそうです。お疲れ様でした。

さいごに
今回、軽い気持ちで三角形の描写をやってみましたが、思ったより計算が多くて私びっくりです。
ここまで読み進めることができた読者がどれくらいか分かりませんが、お疲れ様でした。
latexの数式がうまいこと読み込めなくて、行列表記がうまくいっていないのも申し訳ない限りです。。

